Tanner Tool For Vlsi Design
VLSI Design - Quick Guide
VLSI Design - Digital System
Very-large-scale integration (VLSI) is the process of creating an integrated circuit (IC) by combining thousands of transistors into a single chip. VLSI began in the 1970s when complex semiconductor and communication technologies were being developed. The microprocessor is a VLSI device.
Before the introduction of VLSI technology, most ICs had a limited set of functions they could perform. An electronic circuit might consist of a CPU, ROM, RAM and other glue logic. VLSI lets IC designers add all of these into one chip.
The electronics industry has achieved a phenomenal growth over the last few decades, mainly due to the rapid advances in large scale integration technologies and system design applications. With the advent of very large scale integration (VLSI) designs, the number of applications of integrated circuits (ICs) in high-performance computing, controls, telecommunications, image and video processing, and consumer electronics has been rising at a very fast pace.
The current cutting-edge technologies such as high resolution and low bit-rate video and cellular communications provide the end-users a marvelous amount of applications, processing power and portability. This trend is expected to grow rapidly, with very important implications on VLSI design and systems design.
VLSI Design Flow
The VLSI IC circuits design flow is shown in the figure below. The various levels of design are numbered and the blocks show processes in the design flow.
Specifications comes first, they describe abstractly, the functionality, interface, and the architecture of the digital IC circuit to be designed.
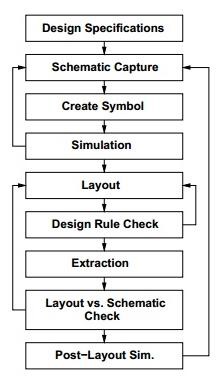
Behavioral description is then created to analyze the design in terms of functionality, performance, compliance to given standards, and other specifications.
RTL description is done using HDLs. This RTL description is simulated to test functionality. From here onwards we need the help of EDA tools.
RTL description is then converted to a gate-level netlist using logic synthesis tools. A gatelevel netlist is a description of the circuit in terms of gates and connections between them, which are made in such a way that they meet the timing, power and area specifications.
Finally, a physical layout is made, which will be verified and then sent to fabrication.
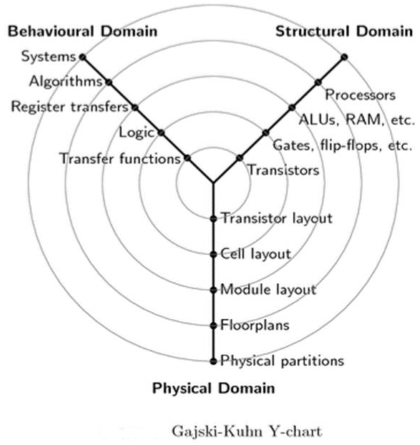
Y Chart
The Gajski-Kuhn Y-chart is a model, which captures the considerations in designing semiconductor devices.
The three domains of the Gajski-Kuhn Y-chart are on radial axes. Each of the domains can be divided into levels of abstraction, using concentric rings.
At the top level (outer ring), we consider the architecture of the chip; at the lower levels (inner rings), we successively refine the design into finer detailed implementation −
Creating a structural description from a behavioral one is achieved through the processes of high-level synthesis or logical synthesis.
Creating a physical description from a structural one is achieved through layout synthesis.
Design Hierarchy-Structural
The design hierarchy involves the principle of "Divide and Conquer." It is nothing but dividing the task into smaller tasks until it reaches to its simplest level. This process is most suitable because the last evolution of design has become so simple that its manufacturing becomes easier.
We can design the given task into the design flow process's domain (Behavioral, Structural, and Geometrical). To understand this, let's take an example of designing a 16-bit adder, as shown in the figure below.
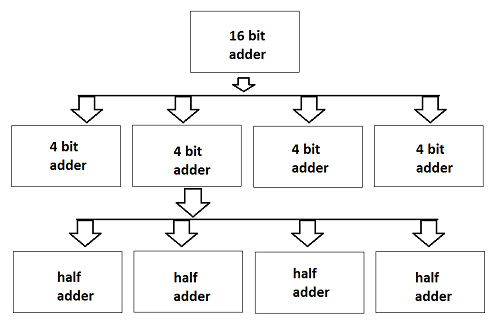
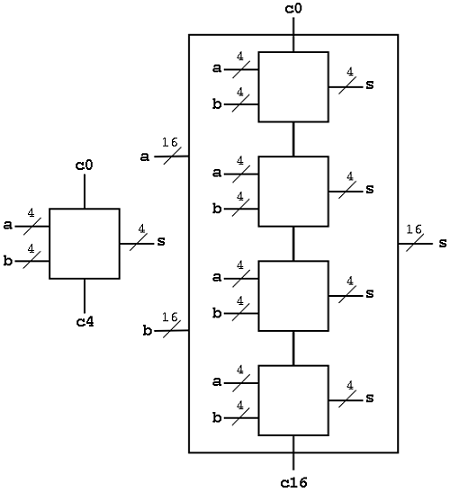
Here, the whole chip of 16 bit adder is divided into four modules of 4-bit adders. Further, dividing the 4-bit adder into 1-bit adder or half adder. 1 bit addition is the simplest designing process and its internal circuit is also easy to fabricate on the chip. Now, connecting all the last four adders, we can design a 4-bit adder and moving on, we can design a 16-bit adder.
VLSI Design - FPGA Technology
FPGA – Introduction
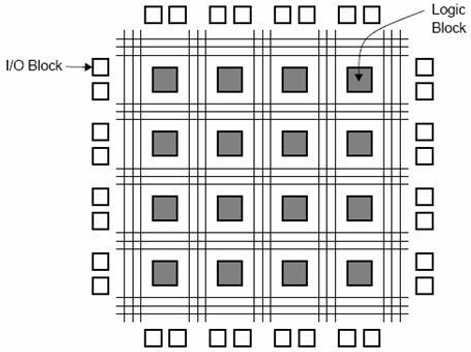
The full form of FPGA is "Field Programmable Gate Array". It contains ten thousand to more than a million logic gates with programmable interconnection. Programmable interconnections are available for users or designers to perform given functions easily. A typical model FPGA chip is shown in the given figure. There are I/O blocks, which are designed and numbered according to function. For each module of logic level composition, there are CLB's (Configurable Logic Blocks).
CLB performs the logic operation given to the module. The inter connection between CLB and I/O blocks are made with the help of horizontal routing channels, vertical routing channels and PSM (Programmable Multiplexers).
The number of CLB it contains only decides the complexity of FPGA. The functionality of CLB's and PSM are designed by VHDL or any other hardware descriptive language. After programming, CLB and PSM are placed on chip and connected with each other with routing channels.
Advantages
- It requires very small time; starting from design process to functional chip.
- No physical manufacturing steps are involved in it.
- The only disadvantage is, it is costly than other styles.
Gate Array Design
The gate array (GA) ranks second after the FPGA, in terms of fast prototyping capability. While user programming is important to the design implementation of the FPGA chip, metal mask design and processing is used for GA. Gate array implementation requires a two-step manufacturing process.
The first phase results in an array of uncommitted transistors on each GA chip. These uncommitted chips can be stored for later customization, which is completed by defining the metal interconnects between the transistors of the array. The patterning of metallic interconnects is done at the end of the chip fabrication process, so that the turn-around time can still be short, a few days to a few weeks. The figure given below shows the basic processing steps for gate array implementation.
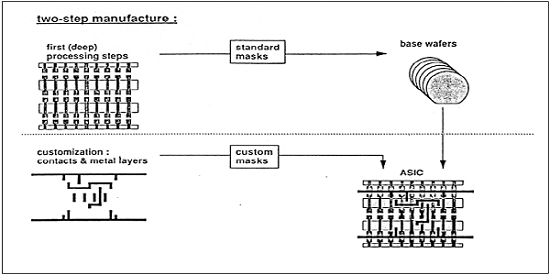
Typical gate array platforms use dedicated areas called channels, for inter-cell routing between rows or columns of MOS transistors. They simplify the interconnections. Interconnection patterns that perform basic logic gates are stored in a library, which can then be used to customize rows of uncommitted transistors according to the netlist.
In most of the modern GAs, multiple metal layers are used for channel routing. With the use of multiple interconnected layers, the routing can be achieved over the active cell areas; so that the routing channels can be removed as in Sea-of-Gates (SOG) chips. Here, the entire chip surface is covered with uncommitted nMOS and pMOS transistors. The neighboring transistors can be customized using a metal mask to form basic logic gates.
For inter cell routing, some of the uncommitted transistors must be sacrificed. This design style results in more flexibility for interconnections and usually in a higher density. GA chip utilization factor is measured by the used chip area divided by the total chip area. It is higher than that of the FPGA and so is the chip speed.
Standard Cell Based Design
A standard cell based design requires development of a full custom mask set. The standard cell is also known as the polycell. In this approach, all of the commonly used logic cells are developed, characterized and stored in a standard cell library.
A library may contain a few hundred cells including inverters, NAND gates, NOR gates, complex AOI, OAI gates, D-latches and Flip-flops. Each gate type can be implemented in several versions to provide adequate driving capability for different fan-outs. The inverter gate can have standard size, double size, and quadruple size so that the chip designer can select the proper size to obtain high circuit speed and layout density.
Each cell is characterized according to several different characterization categories, such as,
- Delay time versus load capacitance
- Circuit simulation model
- Timing simulation model
- Fault simulation model
- Cell data for place-and-route
- Mask data
For automated placement of the cells and routing, each cell layout is designed with a fixed height, so that a number of cells can be bounded side-by-side to form rows. The power and ground rails run parallel to the upper and lower boundaries of the cell. So that, neighboring cells share a common power bus and a common ground bus. The figure shown below is a floorplan for standard-cell based design.

Full Custom Design
In a full-custom design, the entire mask design is made new, without the use of any library. The development cost of this design style is rising. Thus, the concept of design reuse is becoming famous to reduce design cycle time and development cost.
The hardest full custom design can be the design of a memory cell, be it static or dynamic. For logic chip design, a good negotiation can be obtained using a combination of different design styles on the same chip, i.e. standard cells, data-path cells, and programmable logic arrays (PLAs).
Practically, the designer does the full custom layout, i.e. the geometry, orientation, and placement of every transistor. The design productivity is usually very low; typically a few tens of transistors per day, per designer. In digital CMOS VLSI, full-custom design is hardly used due to the high labor cost. These design styles include the design of high-volume products such as memory chips, high-performance microprocessors and FPGA.
VLSI Design - MOS Transistor
Complementary MOSFET (CMOS) technology is widely used today to form circuits in numerous and varied applications. Today's computers, CPUs and cell phones make use of CMOS due to several key advantages. CMOS offers low power dissipation, relatively high speed, high noise margins in both states, and will operate over a wide range of source and input voltages (provided the source voltage is fixed)
For the processes we will discuss, the type of transistor available is the Metal-Oxide-Semiconductor Field Effect Transistor (MOSFET). These transistors are formed as a 'sandwich' consisting of a semiconductor layer, usually a slice, or wafer, from a single crystal of silicon; a layer of silicon dioxide (the oxide) and a layer of metal.
Structure of a MOSFET
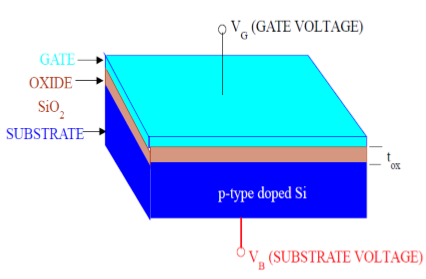
As shown in the figure, MOS structure contains three layers −
-
The Metal Gate Electrode
-
The Insulating Oxide Layer (SiO 2 )
-
P – type Semiconductor (Substrate)
MOS structure forms a capacitor, with gate and substrate are as two plates and oxide layer as the dielectric material. The thickness of dielectric material (SiO 2 ) is usually between 10 nm and 50 nm. Carrier concentration and distribution within the substrate can be manipulated by external voltage applied to gate and substrate terminal. Now, to understand the structure of MOS, first consider the basic electric properties of P – Type semiconductor substrate.
Concentration of carrier in semiconductor material is always following the Mass Action Law. Mass Action Law is given by −
$$n.p=n_{i}^{2}$$
Where,
-
n is carrier concentration of electrons
-
p is carrier concentration of holes
-
ni is intrinsic carrier concentration of Silicon
Now assume that substrate is equally doped with acceptor (Boron) concentration N A . So, electron and hole concentration in p–type substrate is
$$n_{po}=\frac{n_{i}^{2}}{N_{A}}$$
$$p_{po}=N_{A}$$
Here, doping concentration N A is (10 15 to 10 16 cm −3 ) greater than intrinsic concentration ni. Now, to understand the MOS structure, consider the energy level diagram of p–type silicon substrate.
![]()
As shown in the figure, the band gap between conduction band and valance band is 1.1eV. Here, Fermi potential Φ F is the difference between intrinsic Fermi level (E i ) and Fermi level (E FP ).
Where Fermi level E F depends on the doping concentration. Fermi potential Φ F is the difference between intrinsic Fermi level (E i ) and Fermi level (E FP ).
Mathematically,
$$\Phi_{Fp}=\frac{E_{F}-E_{i}}{q}$$
The potential difference between conduction band and free space is called electron affinity and is denoted by qx.
So, energy required for an electron to move from Fermi level to free space is called work function (qΦ S ) and it is given by
$$q\Phi _{s}=(E_{c}-E_{F})+qx$$
The following figure shows the energy band diagram of components that make up the MOS.
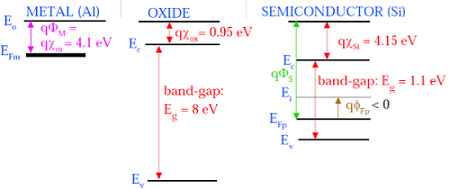
As shown in the above figure, insulating SiO 2 layer has large energy band gap of 8eV and work function is 0.95 eV. Metal gate has work function of 4.1eV. Here, the work functions are different so it will create voltage drop across the MOS system. The figure given below shows the combined energy band diagram of MOS system.
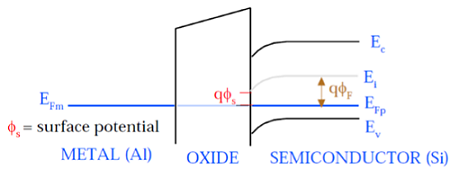
As shown in this figure, the fermi potential level of metal gate and semiconductor (Si) are at same potential. Fermi potential at surface is called surface potential Φ S and it is smaller than Fermi potential Φ F in magnitude.
Working of a MOSFET
MOSFET consists of a MOS capacitor with two p-n junctions placed closed to the channel region and this region is controlled by gate voltage. To make both the p-n junction reverse biased, substrate potential is kept lower than the other three terminals potential.
If the gate voltage will be increased beyond the threshold voltage (V GS >V TO ), inversion layer will be established on the surface and n – type channel will be formed between the source and drain. This n – type channel will carry the drain current according to the V DS value.
For different value of V DS , MOSFET can be operated in different regions as explained below.
Linear Region
At V DS = 0, thermal equilibrium exists in the inverted channel region and drain current I D = 0. Now if small drain voltage, V DS > 0 is applied, a drain current proportional to the V DS will start to flow from source to drain through the channel.
The channel gives a continuous path for the flow of current from source to drain. This mode of operation is called linear region. The cross sectional view of an n-channel MOSFET, operating in linear region, is shown in the figure given below.
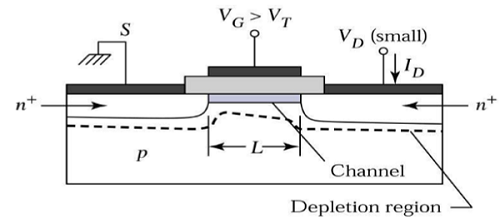
At the Edge of Saturation Region
Now if the V DS is increased, charges in the channel and channel depth decrease at the end of drain. For V DS = V DSAT , the charges in the channel is reduces to zero, which is called pinch – off point. The cross sectional view of n-channel MOSFET operating at the edge of saturation region is shown in the figure given below.
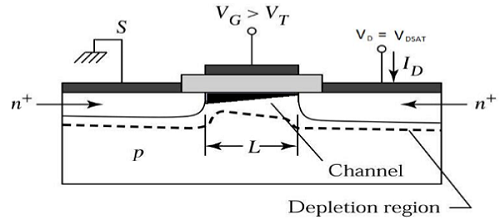
Saturation Region
For V DS >V DSAT , a depleted surface forms near to drain, and by increasing the drain voltage this depleted region extends to source.
This mode of operation is called Saturation region. The electrons coming from the source to the channel end, enter in the drain – depletion region and are accelerated towards the drain in high electric field.
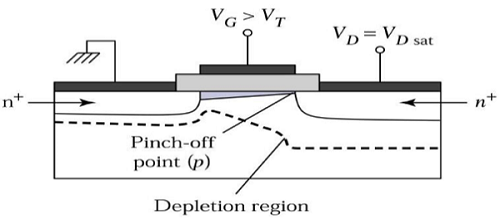
MOSFET Current – Voltage Characteristics
To understand the current – voltage characteristic of MOSFET, approximation for the channel is done. Without this approximation, the three dimension analysis of MOS system becomes complex. The Gradual Channel Approximation (GCA) for current – voltage characteristic will reduce the analysis problem.
Gradual Channel Approximation (GCA)
Consider the cross sectional view of n channel MOSFET operating in the linear mode. Here, source and substrate are connected to the ground. V S = V B = 0. The gate – to – source (V GS ) and drain – to – source voltage (V DS ) voltage are the external parameters that control the drain current I D .
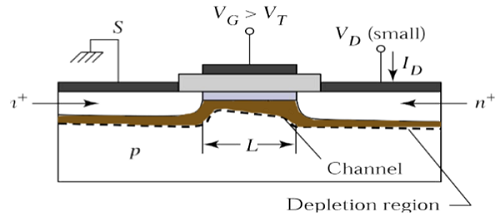
The voltage, V GS is set to a voltage greater than the threshold voltage V TO , to create a channel between the source and drain. As shown in the figure, x – direction is perpendicular to the surface and y – direction is parallel to the surface.
Here, y = 0 at the source end as shown in the figure. The channel voltage, with respect to the source, is represented by V C(Y) . Assume that the threshold voltage VTO is constant along the channel region, between y = 0 to y = L. The boundary condition for the channel voltage V C are −
$$V_{c}\left ( y = 0 \right ) = V_{s} = 0 \,and\,V_{c}\left ( y = L \right ) = V_{DS}$$
We can also assume that
$$V_{GS}\geq V_{TO}$$ and
$$V_{GD} = V_{GS}-V_{DS}\geq V_{TO}$$
Let Q1(y) be the total mobile electron charge in the surface inversion layer. This electron charge can be expressed as −
$$Q1(y)=-C_{ox}.[V_{GS}-V_{C(Y)}-V_{TO}]$$
The figure given below shows the spatial geometry of the surface inversion layer and indicate its dimensions. The inversion layer taper off as we move from drain to source. Now, if we consider the small region dy of channel length L then incremental resistance dR offered by this region can be expressed as −
$$dR=-\frac{dy}{w.\mu _{n}.Q1(y)}$$
Here, minus sign is due to the negative polarity of the inversion layer charge Q1 and μ n is the surface mobility, which is constant. Now, substitute the value of Q1(y) in the dR equation −
$$dR=-\frac{dy}{w.\mu _{n}.\left \{ -C_{ox}\left [ V_{GS}-V_{C\left ( Y \right )} \right ]-V_{TO} \right \}}$$
$$dR=\frac{dy}{w.\mu _{n}.C_{ox}\left [ V_{GS}-V_{C\left ( Y \right )} \right ]-V_{TO}}$$
Now voltage drop in small dy region can be given by
$$dV_{c}=I_{D}.dR$$
Put the value of dR in the above equation
$$dV_{C}=I_{D}.\frac{dy}{w.\mu_{n}.C_{ox}\left [ V_{GS}-V_{C(Y)} \right ]-V_{TO}}$$
$$w.\mu _{n}.C_{ox}\left [ V_{GS}-V_{C(Y)}-V_{TO} \right ].dV_{C}=I_{D}.dy$$
To obtain the drain current ID over the whole channel region, the above equation can be integrated along the channel from y = 0 to y = L and voltages V C(y) = 0 to V C(y) = V DS ,
$$C_{ox}.w.\mu _{n}.\int_{V_{c}=0}^{V_{DS}} \left [ V_{GS}-V_{C\left ( Y \right )}-V_{TO} \right ].dV_{C} = \int_{Y=0}^{L}I_{D}.dy$$
$$\frac{C_{ox}.w.\mu _{n}}{2}\left ( 2\left [ V_{GS}-V_{TO} \right ] V_{DS}-V_{DS}^{2}\right ) = I_{D}\left [ L-0 \right ]$$
$$I_{D} = \frac{C_{ox}.\mu _{n}}{2}.\frac{w}{L}\left ( 2\left [ V_{GS}-V_{TO} \right ]V_{DS}-V_{DS}^{2} \right )$$
For linear region V DS < V GS − V TO . For saturation region, value of V DS is larger than (V GS − V TO ). Therefore, for saturation region V DS = (V GS − V TO ).
$$I_{D} = C_{ox}.\mu _{n}.\frac{w}{2}\left ( \frac{\left [ 2V_{DS} \right ]V_{DS}-V_{DS}^{2}}{L} \right )$$
$$I_{D} = C_{ox}.\mu _{n}.\frac{w}{2}\left ( \frac{2V_{DS}^{2}-V_{DS}^{2}}{L} \right )$$
$$I_{D} = C_{ox}.\mu _{n}.\frac{w}{2}\left ( \frac{V_{DS}^{2}}{L} \right )$$
$$I_{D} = C_{ox}.\mu _{n}.\frac{w}{2}\left ( \frac{\left [ V_{GS}-V_{TO} \right ]^{2}}{L} \right )$$
VLSI Design - MOS Inverter
The inverter is truly the nucleus of all digital designs. Once its operation and properties are clearly understood, designing more intricate structures such as NAND gates, adders, multipliers, and microprocessors is greatly simplified. The electrical behavior of these complex circuits can be almost completely derived by extrapolating the results obtained for inverters.
The analysis of inverters can be extended to explain the behavior of more complex gates such as NAND, NOR, or XOR, which in turn form the building blocks for modules such as multipliers and processors. In this chapter, we focus on one single incarnation of the inverter gate, being the static CMOS inverter — or the CMOS inverter, in short. This is certainly the most popular at present and therefore deserves our special attention.
Principle of Operation
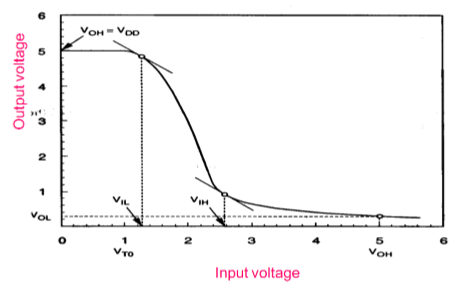
The logic symbol and truth table of ideal inverter is shown in figure given below. Here A is the input and B is the inverted output represented by their node voltages. Using positive logic, the Boolean value of logic 1 is represented by V dd and logic 0 is represented by 0. V th is the inverter threshold voltage, which is V dd /2, where V dd is the output voltage.
The output is switched from 0 to V dd when input is less than V th . So, for 0<V in <V th output is equal to logic 0 input and V th <V in < V dd is equal to logic 1 input for inverter.
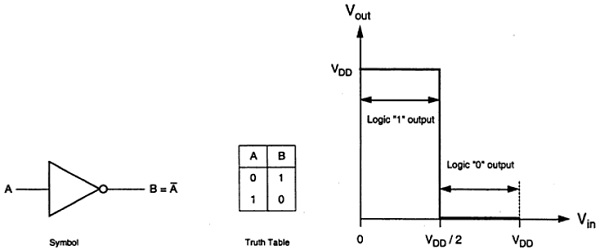
The characteristics shown in the figure are ideal. The generalized circuit structure of an nMOS inverter is shown in the figure below.
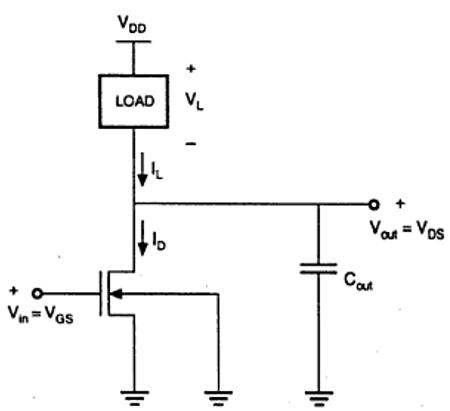
From the given figure, we can see that the input voltage of inverter is equal to the gate to source voltage of nMOS transistor and output voltage of inverter is equal to drain to source voltage of nMOS transistor. The source to substrate voltage of nMOS is also called driver for transistor which is grounded; so V SS = 0. The output node is connected with a lumped capacitance used for VTC.
Resistive Load Inverter
The basic structure of a resistive load inverter is shown in the figure given below. Here, enhancement type nMOS acts as the driver transistor. The load consists of a simple linear resistor R L . The power supply of the circuit is V DD and the drain current I D is equal to the load current I R .
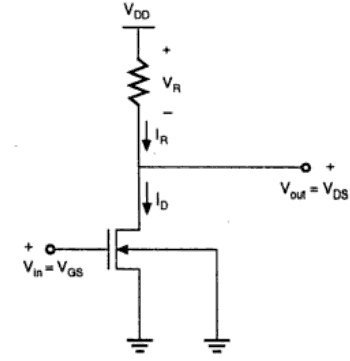
Circuit Operation
When the input of the driver transistor is less than threshold voltage V TH (V in < V TH ), driver transistor is in the cut – off region and does not conduct any current. So, the voltage drop across the load resistor is ZERO and output voltage is equal to the V DD . Now, when the input voltage increases further, driver transistor will start conducting the non-zero current and nMOS goes in saturation region.
Mathematically,
$$I_{D} = \frac{K_{n}}{2}\left [ V_{GS}-V_{TO} \right ]^{2}$$
Increasing the input voltage further, driver transistor will enter into the linear region and output of the driver transistor decreases.
$$I_{D} = \frac{K_{n}}{2}2\left [ V_{GS}-V_{TO} \right ]V_{DS}-V_{DS}^{2}$$
VTC of the resistive load inverter, shown below, indicates the operating mode of driver transistor and voltage points.
Inverter with N type MOSFET Load
The main advantage of using MOSFET as load device is that the silicon area occupied by the transistor is smaller than the area occupied by the resistive load. Here, MOSFET is active load and inverter with active load gives a better performance than the inverter with resistive load.
Enhancement Load NMOS
Two inverters with enhancement-type load device are shown in the figure. Load transistor can be operated either, in saturation region or in linear region, depending on the bias voltage applied to its gate terminal. The saturated enhancement load inverter is shown in the fig. (a). It requires a single voltage supply and simple fabrication process and so V OH is limited to the V DD − V T .
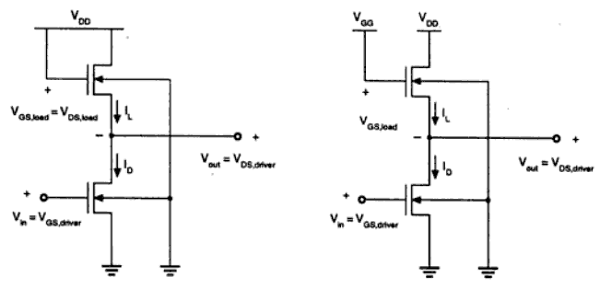
The linear enhancement load inverter is shown in the fig. (b). It always operates in linear region; so V OH level is equal to V DD .
Linear load inverter has higher noise margin compared to the saturated enhancement inverter. But, the disadvantage of linear enhancement inverter is, it requires two separate power supply and both the circuits suffer from high power dissipation. Therefore, enhancement inverters are not used in any large-scale digital applications.
Depletion Load NMOS
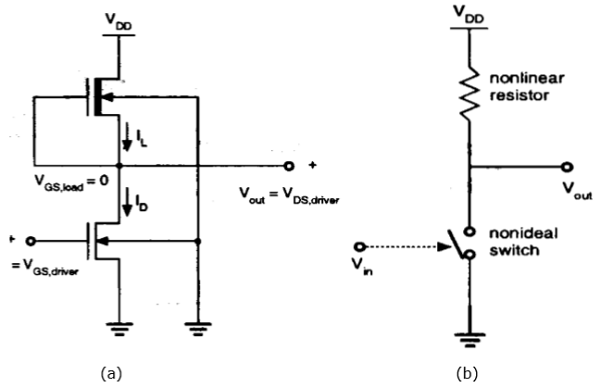
Drawbacks of the enhancement load inverter can be overcome by using depletion load inverter. Compared to enhancement load inverter, depletion load inverter requires few more fabrication steps for channel implant to adjust the threshold voltage of load.
The advantages of the depletion load inverter are - sharp VTC transition, better noise margin, single power supply and smaller overall layout area.
As shown in the figure, the gate and source terminal of load are connected; So, V GS = 0. Thus, the threshold voltage of the load is negative. Hence,
$$V_{GS,load}> V_{T,load}$$ is satisfied
Therefore, load device always has a conduction channel regardless of input and output voltage level.
When the load transistor is in saturation region, the load current is given by
$$I_{D,load} = \frac{K_{n,load}}{2}\left [ -V_{T,load}\left ( V_{out} \right ) \right ]^{2}$$
When the load transistor is in linear region, the load current is given by
$$I_{D,load} = \frac{K_{n,load}}{2}\left [ 2\left | V_{T,load}\left ( V_{out} \right ) \right |.\left ( V_{DD}-V_{out} \right )-\left ( V_{DD}-V_{out} \right )^{2} \right ]$$
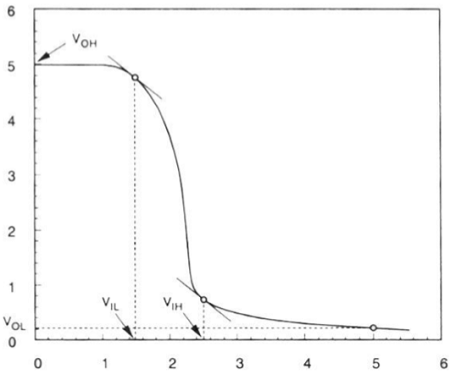
The voltage transfer characteristics of the depletion load inverter is shown in the figure given below −
CMOS Inverter – Circuit, Operation and Description
The CMOS inverter circuit is shown in the figure. Here, nMOS and pMOS transistors work as driver transistors; when one transistor is ON, other is OFF.
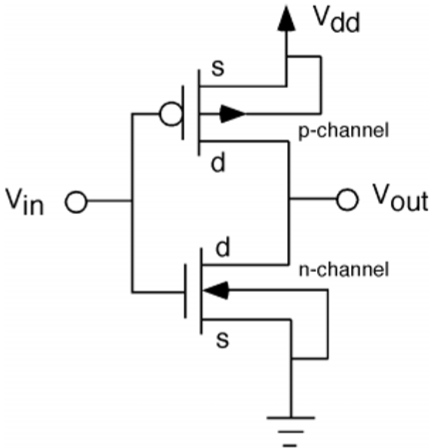
This configuration is called complementary MOS (CMOS). The input is connected to the gate terminal of both the transistors such that both can be driven directly with input voltages. Substrate of the nMOS is connected to the ground and substrate of the pMOS is connected to the power supply, V DD .
So V SB = 0 for both the transistors.
$$V_{GS,n}=V_{in}$$
$$V_{DS,n}=V_{out}$$
And,
$$V_{GS,p}=V_{in}-V_{DD}$$
$$V_{DS,p}=V_{out}-V_{DD}$$
When the input of nMOS is smaller than the threshold voltage (V in < V TO,n ), the nMOS is cut – off and pMOS is in linear region. So, the drain current of both the transistors is zero.
$$I_{D,n}=I_{D,p}=0$$
Therefore, the output voltage V OH is equal to the supply voltage.
$$V_{out}=V_{OH}=V_{DD}$$
When the input voltage is greater than the V DD + V TO,p , the pMOS transistor is in the cutoff region and the nMOS is in the linear region, so the drain current of both the transistors is zero.
$$I_{D,n}=I_{D,p}=0$$
Therefore, the output voltage V OL is equal to zero.
$$V_{out}=V_{OL}=0$$
The nMOS operates in the saturation region if V in > V TO and if following conditions are satisfied.
$$V_{DS,n}\geq V_{GS,n}-V_{TO,n} $$
$$V_{out}\geq V_{in}-V_{TO,n} $$
The pMOS operates in the saturation region if V in < V DD + V TO,p and if following conditions are satisfied.
$$V_{DS,p}\leq V_{GS,p}-V_{TO,p} $$
$$V_{out}\leq V_{in}-V_{TO,p} $$
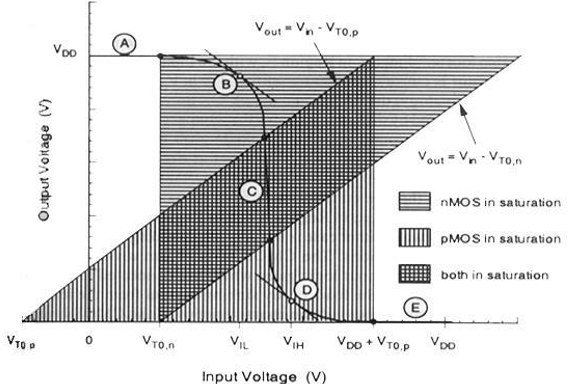
For different value of input voltages, the operating regions are listed below for both transistors.
| Region | V in | V out | nMOS | pMOS |
|---|---|---|---|---|
| A | < V TO, n | V OH | Cut – off | Linear |
| B | V IL | High ≈ V OH | Saturation | Linear |
| C | V th | V th | Saturation | Saturation |
| D | V IH | Low ≈ V OL | Linear | Saturation |
| E | > (V DD + V TO, p ) | V OL | Linear | Cut – off |
The VTC of CMOS is shown in the figure below −
Combinational MOS Logic Circuits
Combinational logic circuits or gates, which perform Boolean operations on multiple input variables and determine the outputs as Boolean functions of the inputs, are the basic building blocks of all digital systems. We will examine simple circuit configurations such as two-input NAND and NOR gates and then expand our analysis to more general cases of multiple-input circuit structures.
Next, the CMOS logic circuits will be presented in a similar fashion. We will stress the similarities and differences between the nMOS depletion-load logic and CMOS logic circuits and point out the advantages of CMOS gates with examples. In its most general form, a combinational logic circuit, or gate, performing a Boolean function can be represented as a multiple-input, single-output system, as depicted in the figure.
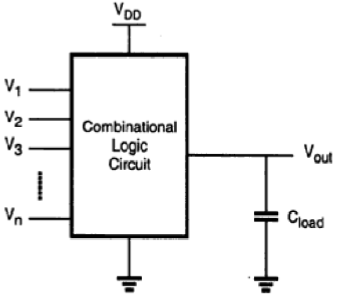
Node voltages, referenced to the ground potential, represent all input variables. Using positive logic convention, the Boolean (or logic) value of "1" can be represented by a high voltage of VDD, and the Boolean (or logic) value of "0" can be represented by a low voltage of 0. The output node is loaded with a capacitance C L , which represents the combined capacitances of the parasitic device in the circuit.
CMOS Logic Circuits
CMOS Two input NOR Gate
The circuit consists of a parallel-connected n-net and a series-connected complementary p-net. The input voltages V X and V Y are applied to the gates of one nMOS and one pMOS transistor.
When either one or both inputs are high, i.e., when the n-net creates a conducting path between the output node and the ground, the p-net is cut—off. If both input voltages are low, i.e., the n-net is cut-off, then the p-net creates a conducting path between the output node and the supply voltage.
For any given input combination, the complementary circuit structure is such that the output is connected either to V DD or to ground via a low-resistance path and a DC current path between the V DD and ground is not established for any input combinations. The output voltage of the CMOS, two input NOR gate will get a logic-low voltage of V OL = 0 and a logic-high voltage of V OH = V DD . The equation of the switching threshold voltage V th is given by
$$V_{th}\left ( NOR2 \right ) = \frac{V_{T,n}+\frac{1}{2}\sqrt{\frac{k_{p}}{k_{n}}\left ( V_{DD}-\left | V_{T,p} \right | \right )}}{1+\frac{1}{2}\sqrt{\frac{k_{p}}{k_{n}}}}$$
Layout of CMOS 2-input NOR Gate
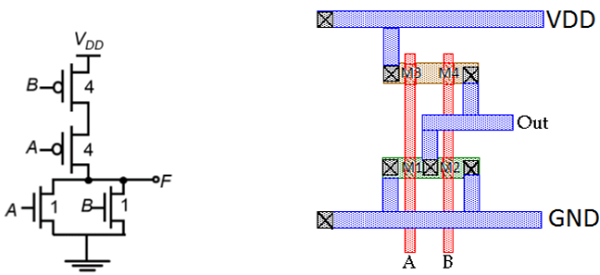
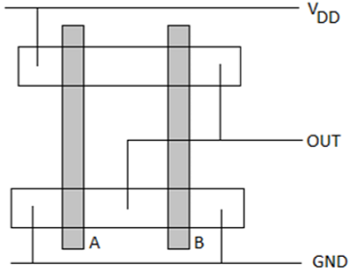
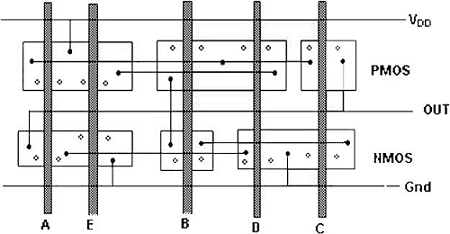
The figure shows a sample layout of CMOS 2-input NOR gate, using single-layer metal and single-layer polysilicon. The features of this layout are −
- Single vertical polylines for each input
- Single active shapes for N and P devices, respectively
- Metal buses running horizontal
The stick diagram for the CMOS N0R2 gate is shown in the figure given below; which corresponds directly to the layout, but does not contain W and L information. The diffusion areas are depicted by rectangles, the metal connections and solid lines and circles, respectively represent contacts, and the crosshatched strips represent the polysilicon columns. Stick diagram is useful for planning optimum layout topology.
CMOS Two-input NAND Gate
The circuit diagram of the two input CMOS NAND gate is given in the figure below.
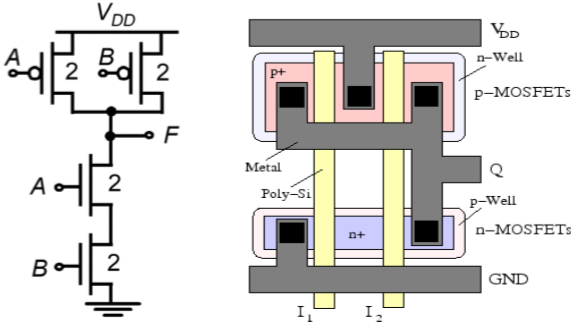
The principle of operation of the circuit is exact dual of the CMOS two input NOR operation. The n – net consisting of two series connected nMOS transistor creates a conducting path between the output node and the ground, if both input voltages are logic high. Both of the parallelly connected pMOS transistor in p-net will be off.
For all other input combination, either one or both of the pMOS transistor will be turn ON, while p – net is cut off, thus, creating a current path between the output node and the power supply voltage. The switching threshold for this gate is obtained as −
$$V_{th}\left ( NAND2 \right ) = \frac{V_{T,n}+2\sqrt{\frac{k_{p}}{k_{n}}\left ( V_{DD}-\left | V_{T,p} \right | \right )}}{1+2\sqrt{\frac{k_{p}}{k_{n}}}}$$
The features of this layout are as follows −
- Single polysilicon lines for inputs run vertically across both N and P active regions.
- Single active shapes are used for building both nMOS devices and both pMOS devices.
- Power bussing is running horizontal across top and bottom of layout.
- Output wires runs horizontal for easy connection to neighboring circuit.
Complex Logic Circuits
NMOS Depletion Load Complex Logic Gate
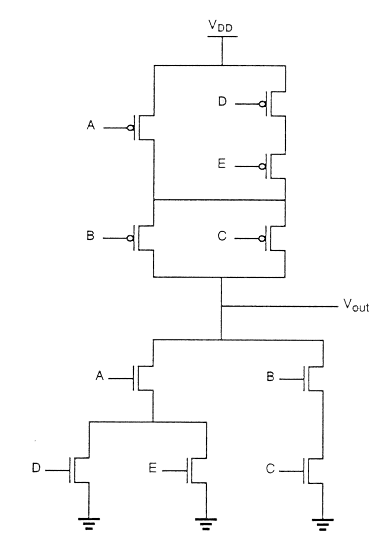
To realize complex functions of multiple input variables, the basic circuit structures and design principles developed for NOR and NAND can be extended to complex logic gates. The ability to realize complex logic functions, using a small number of transistors is one of the most attractive features of nMOS and CMOS logic circuits. Consider the following Boolean function as an example.
$$\overline{Z=P\left ( S+T \right )+QR}$$
The nMOS depletion-load complex logic gate used to realize this function is shown in figure. In this figure, the left nMOS driver branch of three driver transistors is used to perform the logic function P (S + T), while the right-hand side branch performs the function QR. By connecting the two branches in parallel, and by placing the load transistor between the output node and the supply voltage V DD , we obtain the given complex function. Each input variable is assigned to only one driver.
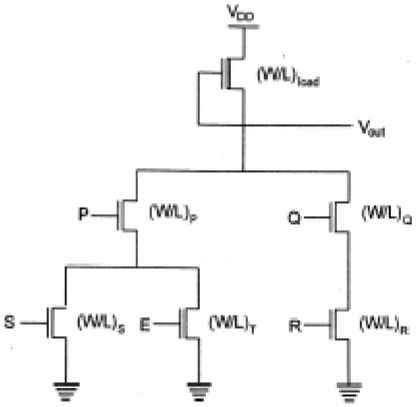
Inspection of the circuit topology gives simple design principles of the pull-down network −
- OR operations are performed by parallel-connected drivers.
- AND operations are performed by series-connected drivers.
- Inversion is provided by the nature of MOS circuit operation.
If all input variables are logic-high in the circuit realizing the function, the equivalent driver (W/L) ratio of the pull-down network consisting of five nMOS transistors is
$$\frac{W}{L}=\frac{1}{\frac{1}{\left ( W/L \right )Q}+\frac{1}{\left ( W/L \right )R}}+\frac{1}{\frac{1}{\left ( W/L \right )P}+\frac{1}{\left ( W/L \right )S+\left ( W/L \right )Q}}$$
Complex CMOS Logic Gates
The realization of the n-net, or pull-down network, is based on the same basic design principles examined for nMOS depletion-load complex logic gate. The pMOS pull-up network must be the dual network of the n-net.
It means all parallel connections in the nMOS network will correspond to a series connection in the pMOS network, and all series connection in the nMOS network correspond to a parallel connection in the pMOS network. The figure shows a simple construction of the dual p-net (pull-up) graph from the n-net (pull-down) graph.
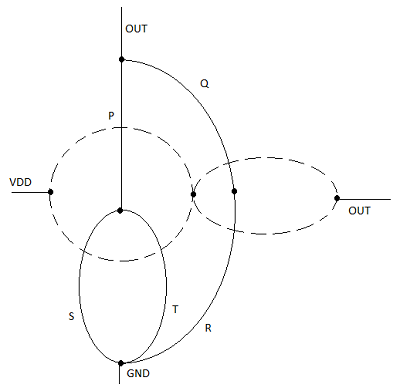
Each driver transistor in the pull-down network is shown by ai and each node is shown by a vertex in the pull-down graph. Next, a new vertex is created within each confined area in the pull graph, and neighboring vertices are connected by edges which cross each edge in the pull-down graph only once. This new graph shows the pull-up network.
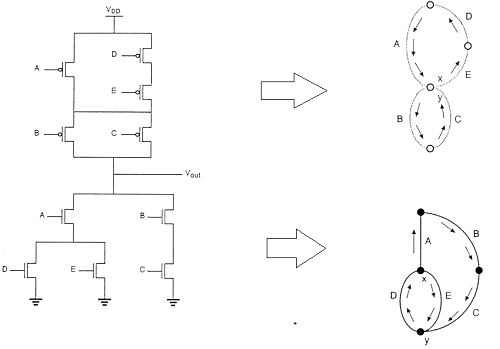
Layout Technique using Euler Graph Method
The figure shows the CMOS implementation of a complex function and its stick diagram done with arbitrary gate ordering that gives a very non-optimum layout for the CMOS gate.
In this case, the separation between the polysilicon columns must allow diffusion-todiffusion separation in between. This certainly consumes a considerably amount of extra silicon area.
By using the Euler path, we can obtain an optimum layout. The Euler path is defined as an uninterrupted path that traverses each edge (branch) of the graph exactly once. Find Euler path in both the pull-down tree graph and the pull-up tree graph with identical ordering of the inputs.
VLSI Design - Sequential MOS Logic Circuits
Logic circuits are divided into two categories − (a) Combinational Circuits, and (b) Sequential Circuits.
In Combinational circuits, the output depends only on the condition of the latest inputs.
In Sequential circuits, the output depends not only on the latest inputs, but also on the condition of earlier inputs. Sequential circuits contain memory elements.
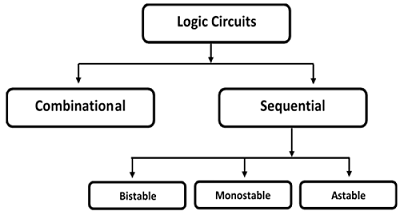
Sequential circuits are of three types −
Bistable − Bistable circuits have two stable operating points and will be in either of the states. Example − Memory cells, latches, flip-flops and registers.
Monostable − Monostable circuits have only one stable operating point and even if they are temporarily perturbed to the opposite state, they will return in time to their stable operating point. Example: Timers, pulse generators.
Astable − circuits have no stable operating point and oscillate between several states. Example − Ring oscillator.
CMOS Logic Circuits
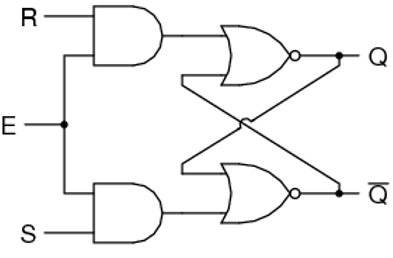
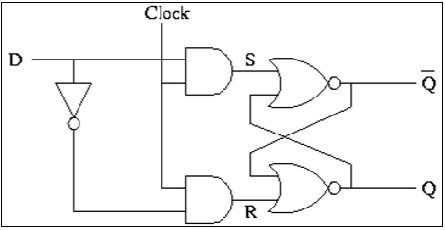
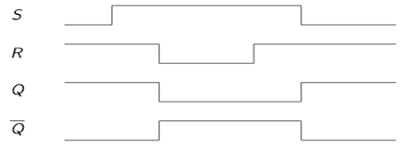
SR Latch based on NOR Gate
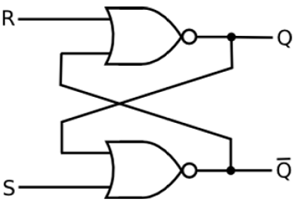
If the set input (S) is equal to logic "1" and the reset input is equal to logic "0." then the output Q will be forced to logic "1". While $\overline{Q}$ is forced to logic "0". This means the SR latch will be set, irrespective of its previous state.
Similarly, if S is equal to "0" and R is equal to "1" then the output Q will be forced to "0" while $\overline{Q}$ is forced to "1". This means the latch is reset, regardless of its previously held state. Finally, if both of the inputs S and R are equal to logic "1" then both output will be forced to logic "0" which conflicts with the complementarity of Q and $\overline{Q}$.
Therefore, this input combination is not allowed during normal operation. Truth table of NOR based SR Latch is given in table.
| S | R | Q | $\overline{Q}$ | Operation |
|---|---|---|---|---|
| 0 | 0 | Q | $\overline{Q}$ | Hold |
| 1 | 0 | 1 | 0 | Set |
| 0 | 1 | 0 | 1 | Reset |
| 1 | 1 | 0 | 0 | Not allowed |
CMOS SR latch based on NOR gate is shown in the figure given below.
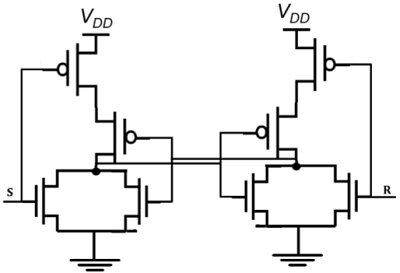
If the S is equal to V OH and the R is equal to V OL , both of the parallel-connected transistors M1 and M2 will be ON. The voltage on node $\overline{Q}$ will assume a logic-low level of V OL = 0.
At the same time, both M3 and M4 are turned off, which results in a logic-high voltage V OH at node Q. If the R is equal to V OH and the S is equal to V OL , M1 and M2 turned off and M3 and M4 turned on.
SR Latch based on NAND Gate
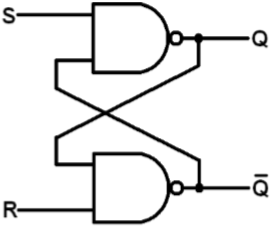
Block diagram and gate level schematic of NAND based SR latch is shown in the figure. The small circles at the S and R input terminals represents that the circuit responds to active low input signals. The truth table of NAND based SR latch is given in table
| S | R | Q | Q′ | |
| 0 | 0 | NC | NC | No change. Latch remained in present state. |
| 1 | 0 | 1 | 0 | Latch SET. |
| 0 | 1 | 0 | 1 | Latch RESET. |
| 1 | 1 | 0 | 0 | Invalid condition. |
If S goes to 0 (while R = 1), Q goes high, pulling $\overline{Q}$ low and the latch enters Set state
S = 0 then Q = 1 (if R = 1)
If R goes to 0 (while S = 1), Q goes high, pulling $\overline{Q}$ low and the latch is Reset
R = 0 then Q = 1 (if S = 1)
Hold state requires both S and R to be high. If S = R = 0 then output is not allowed, as it would result in an indeterminate state. CMOS SR Latch based on NAND Gate is shown in figure.
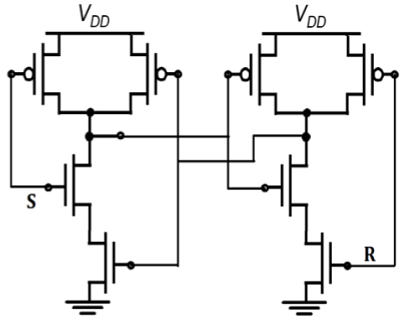
Depletion-load nMOS SR Latch based on NAND Gate is shown in figure. The operation is similar to that of CMOS NAND SR latch. The CMOS circuit implementation has low static power dissipation and high noise margin.
CMOS Logic Circuits
Clocked SR Latch
The figure shows a NOR-based SR latch with a clock added. The latch is responsive to inputs S and R only when CLK is high.
When CLK is low, the latch retains its current state. Observe that Q changes state −
- When S goes high during positive CLK.
- On leading CLK edge after changes in S & R during CLK low time.
- A positive glitch in S while CLK is high
- When R goes high during positive CLK.
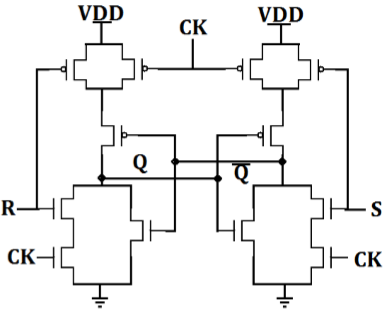
CMOS AOI implementation of clocked NOR based SR latch is shown in the figure. Note that only 12 transistors required.
-
When CLK is low, two series terminals in N tree N are open and two parallel transistors in tree P are ON, thus retaining state in the memory cell.
-
When clock is high, the circuit becomes simply a NOR based CMOS latch which will respond to input S and R.
Clocked SR Latch based on NAND Gate
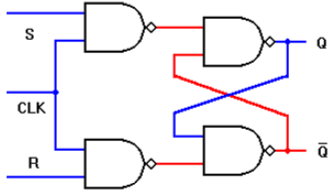
Circuit is implemented with four NAND gates. If this circuit is implemented with CMOS then it requires 16 transistors.
- The latch is responsive to S or R only if CLK is high.
- If both input signals and the CLK signals are active high: i.e., the latch output Q will be set when CLK = "1" S = "1" and R = "0"
- Similarly, the latch will be reset when CLK = "1," S = "0," and
When CLK is low, the latch retains its present state.
Clocked JK Latch
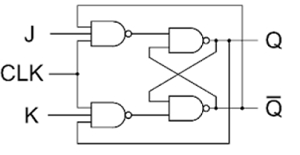
The figure above shows a clocked JK latch, based on NAND gates. The disadvantage of an SR latch is that when both S and R are high, its output state becomes indeterminant. The JK latch eliminates this problem by using feedback from output to input, such that all input states of the truth table are allowable. If J = K = 0, the latch will hold its present state.
If J = 1 and K = 0, the latch will set on the next positive-going clock edge, i.e. Q = 1, $\overline{Q}$ = 0
If J = 0 and K = 1, the latch will reset on the next positive-going clock edge, i.e. Q = 1 and $\overline{Q}$ = 0.
If J = K = 1, the latch will toggle on the next positive-going clock edge
The operation of the clocked JK latch is summarized in the truth table given in table.
| J | K | Q | $\overline{Q}$ | S | R | Q | $\overline{Q}$ | Operation |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | Hold |
| 1 | 0 | 1 | 1 | 1 | 0 | |||
| 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | Reset |
| 1 | 0 | 1 | 0 | 0 | 1 | |||
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | Set |
| 1 | 0 | 1 | 1 | 1 | 0 | |||
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | toggle |
| 1 | 0 | 1 | 0 | 0 | 1 |
CMOS D Latch Implementation
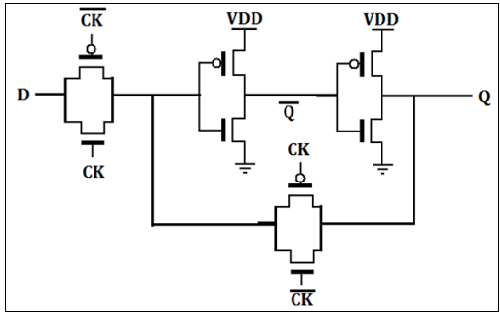
The D latch is normally, implemented with transmission gate (TG) switches as shown in the figure. The input TG is activated with CLK while the latch feedback loop TG is activated with CLK. Input D is accepted when CLK is high. When CLK goes low, the input is opencircuited and the latch is set with the prior data D.
VLSI Design - VHDL Introduction
VHDL stands for very high-speed integrated circuit hardware description language. It is a programming language used to model a digital system by dataflow, behavioral and structural style of modeling. This language was first introduced in 1981 for the department of Defense (DoD) under the VHSIC program.
Describing a Design
In VHDL an entity is used to describe a hardware module. An entity can be described using,
- Entity declaration
- Architecture
- Configuration
- Package declaration
- Package body
Let's see what are these?
Entity Declaration
It defines the names, input output signals and modes of a hardware module.
Syntax −
entity entity_name is Port declaration; end entity_name;
An entity declaration should start with 'entity' and end with 'end' keywords. The direction will be input, output or inout.
| In | Port can be read |
| Out | Port can be written |
| Inout | Port can be read and written |
| Buffer | Port can be read and written, it can have only one source. |
Architecture −
Architecture can be described using structural, dataflow, behavioral or mixed style.
Syntax −
architecture architecture_name of entity_name architecture_declarative_part; begin Statements; end architecture_name;
Here, we should specify the entity name for which we are writing the architecture body. The architecture statements should be inside the 'begin' and 'énd' keyword. Architecture declarative part may contain variables, constants, or component declaration.
Data Flow Modeling
In this modeling style, the flow of data through the entity is expressed using concurrent (parallel) signal. The concurrent statements in VHDL are WHEN and GENERATE.
Besides them, assignments using only operators (AND, NOT, +, *, sll, etc.) can also be used to construct code.
Finally, a special kind of assignment, called BLOCK, can also be employed in this kind of code.
In concurrent code, the following can be used −
- Operators
- The WHEN statement (WHEN/ELSE or WITH/SELECT/WHEN);
- The GENERATE statement;
- The BLOCK statement
Behavioral Modeling
In this modeling style, the behavior of an entity as set of statements is executed sequentially in the specified order. Only statements placed inside a PROCESS, FUNCTION, or PROCEDURE are sequential.
PROCESSES, FUNCTIONS, and PROCEDURES are the only sections of code that are executed sequentially.
However, as a whole, any of these blocks is still concurrent with any other statements placed outside it.
One important aspect of behavior code is that it is not limited to sequential logic. Indeed, with it, we can build sequential circuits as well as combinational circuits.
The behavior statements are IF, WAIT, CASE, and LOOP. VARIABLES are also restricted and they are supposed to be used in sequential code only. VARIABLE can never be global, so its value cannot be passed out directly.
Structural Modeling
In this modeling, an entity is described as a set of interconnected components. A component instantiation statement is a concurrent statement. Therefore, the order of these statements is not important. The structural style of modeling describes only an interconnection of components (viewed as black boxes), without implying any behavior of the components themselves nor of the entity that they collectively represent.
In Structural modeling, architecture body is composed of two parts − the declarative part (before the keyword begin) and the statement part (after the keyword begin).
Logic Operation – AND GATE
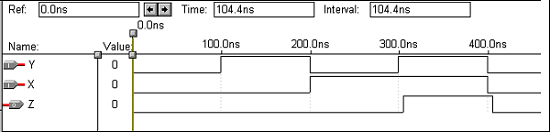
| X | Y | Z |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
VHDL Code: Library ieee; use ieee.std_logic_1164.all; entity and1 is port(x,y:in bit ; z:out bit); end and1; architecture virat of and1 is begin z<=x and y; end virat;
Waveforms
Logic Operation – OR Gate
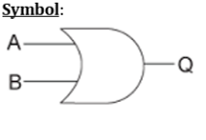
| X | Y | Z |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
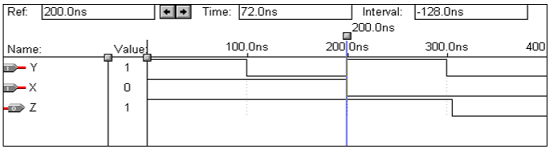
VHDL Code: Library ieee; use ieee.std_logic_1164.all; entity or1 is port(x,y:in bit ; z:out bit); end or1; architecture virat of or1 is begin z<=x or y; end virat;
Waveforms
Logic Operation – NOT Gate
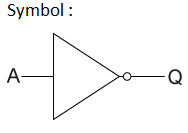
| X | Y |
|---|---|
| 0 | 1 |
| 1 | 0 |
VHDL Code: Library ieee; use ieee.std_logic_1164.all; entity not1 is port(x:in bit ; y:out bit); end not1; architecture virat of not1 is begin y<=not x; end virat;
Waveforms
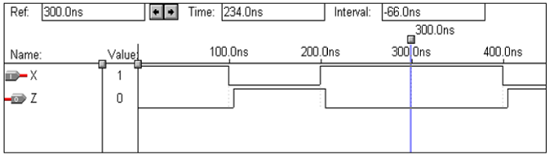
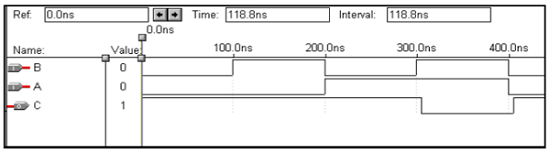
Logic Operation – NAND Gate
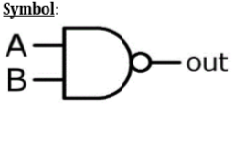
| X | Y | z |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
VHDL Code: Library ieee; use ieee.std_logic_1164.all; entity nand1 is port(a,b:in bit ; c:out bit); end nand1; architecture virat of nand1 is begin c<=a nand b; end virat;
Waveforms
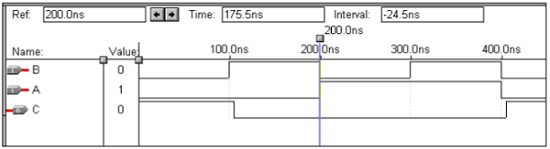
Logic Operation – NOR Gate
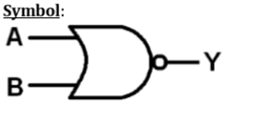
| X | Y | z |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
VHDL Code: Library ieee; use ieee.std_logic_1164.all; entity nor1 is port(a,b:in bit ; c:out bit); end nor1; architecture virat of nor1 is begin c<=a nor b; end virat;
Waveforms
Logic Operation – XOR Gate
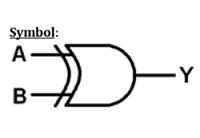
| X | Y | Z |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
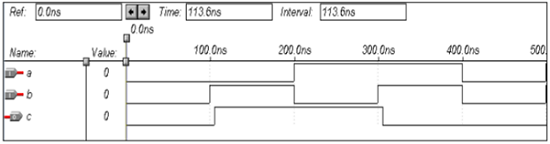
VHDL Code: Library ieee; use ieee.std_logic_1164.all; entity xor1 is port(a,b:in bit ; c:out bit); end xor1; architecture virat of xor1 is begin c<=a xor b; end virat;
Waveforms
Logic Operation – X-NOR Gate
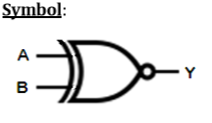
| X | Y | Z |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
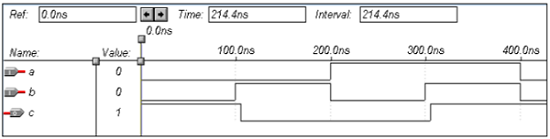
VHDL Code: Library ieee; use ieee.std_logic_1164.all; entity xnor1 is port(a,b:in bit ; c:out bit); end xnor1; architecture virat of xnor1 is begin c<=not(a xor b); end virat;
Waveforms
VHDL Programming Combinational Circuits
This chapter explains the VHDL programming for Combinational Circuits.
VHDL Code for a Half-Adder
VHDL Code: Library ieee; use ieee.std_logic_1164.all; entity half_adder is port(a,b:in bit; sum,carry:out bit); end half_adder; architecture data of half_adder is begin sum<= a xor b; carry <= a and b; end data;
Waveforms
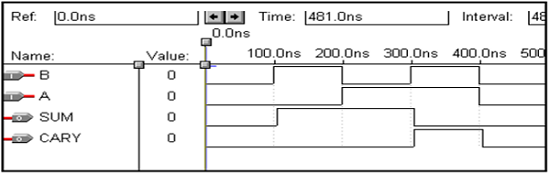
VHDL Code for a Full Adder
Library ieee; use ieee.std_logic_1164.all; entity full_adder is port(a,b,c:in bit; sum,carry:out bit); end full_adder; architecture data of full_adder is begin sum<= a xor b xor c; carry <= ((a and b) or (b and c) or (a and c)); end data;
Waveforms
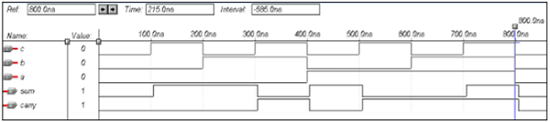
VHDL Code for a Half-Subtractor
Library ieee; use ieee.std_logic_1164.all; entity half_sub is port(a,c:in bit; d,b:out bit); end half_sub; architecture data of half_sub is begin d<= a xor c; b<= (a and (not c)); end data;
Waveforms
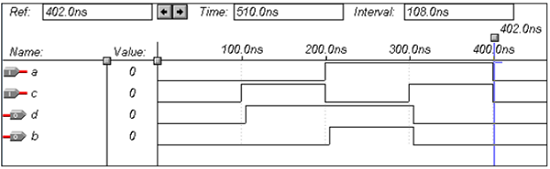
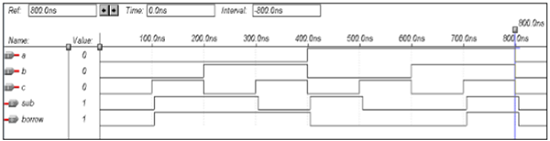
VHDL Code for a Full Subtractor
Library ieee; use ieee.std_logic_1164.all; entity full_sub is port(a,b,c:in bit; sub,borrow:out bit); end full_sub; architecture data of full_sub is begin sub<= a xor b xor c; borrow <= ((b xor c) and (not a)) or (b and c); end data;
Waveforms
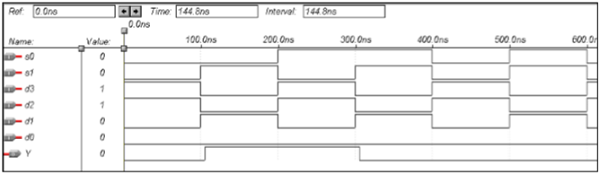
VHDL Code for a Multiplexer
Library ieee; use ieee.std_logic_1164.all; entity mux is port(S1,S0,D0,D1,D2,D3:in bit; Y:out bit); end mux; architecture data of mux is begin Y<= (not S0 and not S1 and D0) or (S0 and not S1 and D1) or (not S0 and S1 and D2) or (S0 and S1 and D3); end data;
Waveforms
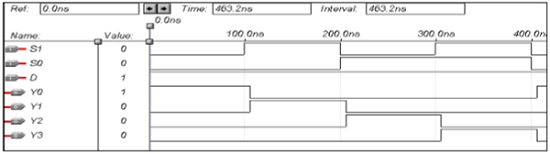
VHDL Code for a Demultiplexer
Library ieee; use ieee.std_logic_1164.all; entity demux is port(S1,S0,D:in bit; Y0,Y1,Y2,Y3:out bit); end demux; architecture data of demux is begin Y0<= ((Not S0) and (Not S1) and D); Y1<= ((Not S0) and S1 and D); Y2<= (S0 and (Not S1) and D); Y3<= (S0 and S1 and D); end data;
Waveforms
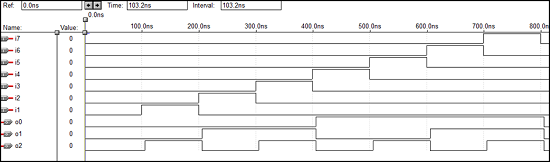
VHDL Code for a 8 x 3 Encoder
library ieee; use ieee.std_logic_1164.all; entity enc is port(i0,i1,i2,i3,i4,i5,i6,i7:in bit; o0,o1,o2: out bit); end enc; architecture vcgandhi of enc is begin o0<=i4 or i5 or i6 or i7; o1<=i2 or i3 or i6 or i7; o2<=i1 or i3 or i5 or i7; end vcgandhi;
Waveforms
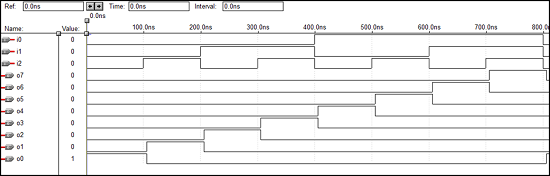
VHDL Code for a 3 x 8 Decoder
library ieee; use ieee.std_logic_1164.all; entity dec is port(i0,i1,i2:in bit; o0,o1,o2,o3,o4,o5,o6,o7: out bit); end dec; architecture vcgandhi of dec is begin o0<=(not i0) and (not i1) and (not i2); o1<=(not i0) and (not i1) and i2; o2<=(not i0) and i1 and (not i2); o3<=(not i0) and i1 and i2; o4<=i0 and (not i1) and (not i2); o5<=i0 and (not i1) and i2; o6<=i0 and i1 and (not i2); o7<=i0 and i1 and i2; end vcgandhi;
Waveforms
VHDL Code – 4 bit Parallel adder
library IEEE; use IEEE.STD_LOGIC_1164.all; entity pa is port(a : in STD_LOGIC_VECTOR(3 downto 0); b : in STD_LOGIC_VECTOR(3 downto 0); ca : out STD_LOGIC; sum : out STD_LOGIC_VECTOR(3 downto 0) ); end pa; architecture vcgandhi of pa is Component fa is port (a : in STD_LOGIC; b : in STD_LOGIC; c : in STD_LOGIC; sum : out STD_LOGIC; ca : out STD_LOGIC ); end component; signal s : std_logic_vector (2 downto 0); signal temp: std_logic; begin temp<='0'; u0 : fa port map (a(0),b(0),temp,sum(0),s(0)); u1 : fa port map (a(1),b(1),s(0),sum(1),s(1)); u2 : fa port map (a(2),b(2),s(1),sum(2),s(2)); ue : fa port map (a(3),b(3),s(2),sum(3),ca); end vcgandhi;
Waveforms

VHDL Code – 4 bit Parity Checker
library ieee; use ieee.std_logic_1164.all; entity parity_checker is port (a0,a1,a2,a3 : in std_logic; p : out std_logic); end parity_checker; architecture vcgandhi of parity_checker is begin p <= (((a0 xor a1) xor a2) xor a3); end vcgandhi;
Waveforms
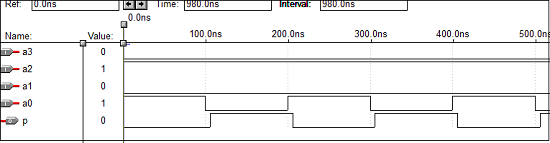
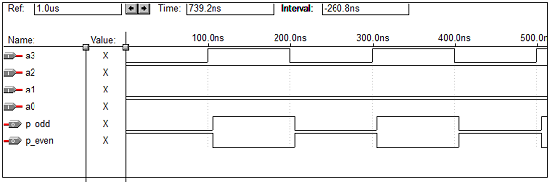
VHDL Code – 4 bit Parity Generator
library ieee; use ieee.std_logic_1164.all; entity paritygen is port (a0, a1, a2, a3: in std_logic; p_odd, p_even: out std_logic); end paritygen; architecture vcgandhi of paritygen is begin process (a0, a1, a2, a3) if (a0 ='0' and a1 ='0' and a2 ='0' and a3 ='0') then odd_out <= "0"; even_out <= "0"; else p_odd <= (((a0 xor a1) xor a2) xor a3); p_even <= not(((a0 xor a1) xor a2) xor a3); end vcgandhi
Waveforms
VHDL Programming for Sequential Circuits
This chapter explains how to do VHDL programming for Sequential Circuits.
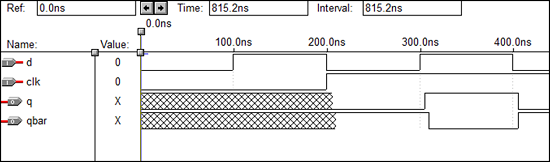
VHDL Code for an SR Latch
library ieee; use ieee.std_logic_1164.all; entity srl is port(r,s:in bit; q,qbar:buffer bit); end srl; architecture virat of srl is signal s1,r1:bit; begin q<= s nand qbar; qbar<= r nand q; end virat;
Waveforms
VHDL Code for a D Latch
library ieee; use ieee.std_logic_1164.all; entity Dl is port(d:in bit; q,qbar:buffer bit); end Dl; architecture virat of Dl is signal s1,r1:bit; begin q<= d nand qbar; qbar<= d nand q; end virat;
Waveforms
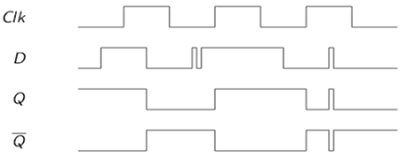
VHDL Code for an SR Flip Flop
library ieee; use ieee.std_logic_1164.all; entity srflip is port(r,s,clk:in bit; q,qbar:buffer bit); end srflip; architecture virat of srflip is signal s1,r1:bit; begin s1<=s nand clk; r1<=r nand clk; q<= s1 nand qbar; qbar<= r1 nand q; end virat;
Waveforms

VHDL code for a JK Flip Flop
library IEEE; use IEEE.STD_LOGIC_1164.all; entity jk is port( j : in STD_LOGIC; k : in STD_LOGIC; clk : in STD_LOGIC; reset : in STD_LOGIC; q : out STD_LOGIC; qb : out STD_LOGIC ); end jk; architecture virat of jk is begin jkff : process (j,k,clk,reset) is variable m : std_logic := '0'; begin if (reset = '1') then m : = '0'; elsif (rising_edge (clk)) then if (j/ = k) then m : = j; elsif (j = '1' and k = '1') then m : = not m; end if; end if; q <= m; qb <= not m; end process jkff; end virat;
Waveforms
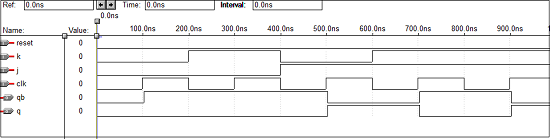
VHDL Code for a D Flip Flop
Library ieee; use ieee.std_logic_1164.all; entity dflip is port(d,clk:in bit; q,qbar:buffer bit); end dflip; architecture virat of dflip is signal d1,d2:bit; begin d1<=d nand clk; d2<=(not d) nand clk; q<= d1 nand qbar; qbar<= d2 nand q; end virat;
Waveforms
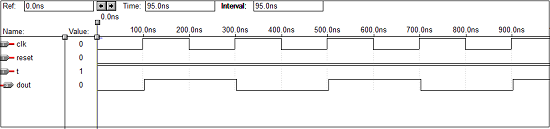
VHDL Code for a T Flip Flop
library IEEE; use IEEE.STD_LOGIC_1164.all; entity Toggle_flip_flop is port( t : in STD_LOGIC; clk : in STD_LOGIC; reset : in STD_LOGIC; dout : out STD_LOGIC ); end Toggle_flip_flop; architecture virat of Toggle_flip_flop is begin tff : process (t,clk,reset) is variable m : std_logic : = '0'; begin if (reset = '1') then m : = '0'; elsif (rising_edge (clk)) then if (t = '1') then m : = not m; end if; end if; dout < = m; end process tff; end virat;
Waveforms
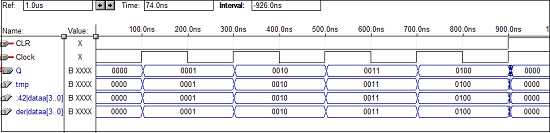
VHDL Code for a 4 - bit Up Counter
library IEEE; use ieee.std_logic_1164.all; use ieee.std_logic_unsigned.all; entity counter is port(Clock, CLR : in std_logic; Q : out std_logic_vector(3 downto 0) ); end counter; architecture virat of counter is signal tmp: std_logic_vector(3 downto 0); begin process (Clock, CLR) begin if (CLR = '1') then tmp < = "0000"; elsif (Clock'event and Clock = '1') then mp <= tmp + 1; end if; end process; Q <= tmp; end virat;
Waveforms
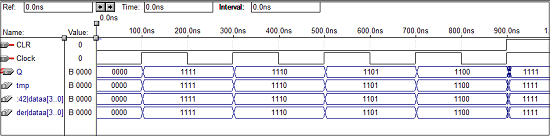
VHDL Code for a 4-bit Down Counter
library ieee; use ieee.std_logic_1164.all; use ieee.std_logic_unsigned.all; entity dcounter is port(Clock, CLR : in std_logic; Q : out std_logic_vector(3 downto 0)); end dcounter; architecture virat of dcounter is signal tmp: std_logic_vector(3 downto 0); begin process (Clock, CLR) begin if (CLR = '1') then tmp <= "1111"; elsif (Clock'event and Clock = '1') then tmp <= tmp - 1; end if; end process; Q <= tmp; end virat;
Waveforms
VLSI Design - Verilog Introduction
Verilog is a HARDWARE DESCRIPTION LANGUAGE (HDL). It is a language used for describing a digital system like a network switch or a microprocessor or a memory or a flip−flop. It means, by using a HDL we can describe any digital hardware at any level. Designs, which are described in HDL are independent of technology, very easy for designing and debugging, and are normally more useful than schematics, particularly for large circuits.
Verilog supports a design at many levels of abstraction. The major three are −
- Behavioral level
- Register-transfer level
- Gate level
Behavioral level
This level describes a system by concurrent algorithms (Behavioural). Every algorithm is sequential, which means it consists of a set of instructions that are executed one by one. Functions, tasks and blocks are the main elements. There is no regard to the structural realization of the design.
Register−Transfer Level
Designs using the Register−Transfer Level specify the characteristics of a circuit using operations and the transfer of data between the registers. Modern definition of an RTL code is "Any code that is synthesizable is called RTL code".
Gate Level
Within the logical level, the characteristics of a system are described by logical links and their timing properties. All signals are discrete signals. They can only have definite logical values (`0', `1', `X', `Z`). The usable operations are predefined logic primitives (basic gates). Gate level modelling may not be a right idea for logic design. Gate level code is generated using tools like synthesis tools and his netlist is used for gate level simulation and for backend.
Lexical Tokens
Verilog language source text files are a stream of lexical tokens. A token consists of one or more characters, and each single character is in exactly one token.
The basic lexical tokens used by the Verilog HDL are similar to those in C Programming Language. Verilog is case sensitive. All the key words are in lower case.
White Space
White spaces can contain characters for spaces, tabs, new-lines and form feeds. These characters are ignored except when they serve to separate tokens.
White space characters are Blank space, Tabs, Carriage returns, New line, and Form feeds.
Comments
There are two forms to represent the comments
- 1) Single line comments begin with the token // and end with carriage return.
Ex.: //this is single line syntax
- 2) Multiline comments begins with the token /* and end with token */
Ex.: /* this is multiline Syntax*/
Numbers
You can specify a number in binary, octal, decimal or hexadecimal format. Negative numbers are represented in 2's compliment numbers. Verilog allows integers, real numbers and signed & unsigned numbers.
The syntax is given by − <size> <radix> <value>
Size or unsized number can be defined in <Size> and <radix> defines whether it is binary, octal, hexadecimal or decimal.
Identifiers
Identifier is the name used to define the object, such as a function, module or register. Identifiers should begin with an alphabetical characters or underscore characters. Ex. A_Z, a_z,_
Identifiers are a combination of alphabetic, numeric, underscore and $ characters. They can be up to 1024 characters long.
Operators
Operators are special characters used to put conditions or to operate the variables. There are one, two and sometimes three characters used to perform operations on variables.
Ex. >, +, ~, &! =.
Verilog Keywords
Words that have special meaning in Verilog are called the Verilog keywords. For example, assign, case, while, wire, reg, and, or, nand, and module. They should not be used as identifiers. Verilog keywords also include compiler directives, and system tasks and functions.
Gate Level Modelling
Verilog has built-in primitives like logic gates, transmission gates and switches. These are rarely used for design work but they are used in post synthesis world for modelling of ASIC/FPGA cells.
Gate level modelling exhibits two properties −
Drive strength − The strength of the output gates is defined by drive strength. The output is strongest if there is a direct connection to the source. The strength decreases if the connection is via a conducting transistor and least when connected via a pull-up/down resistive. The drive strength is usually not specified, in which case the strengths defaults to strong1 and strong0.
Delays − If delays are not specified, then the gates do not have propagation delays; if two delays are specified, then first one represents the rise delay and the second one, fall delay; if only one delay is specified, then both, rise and fall are equal. Delays can be ignored in synthesis.
Gate Primitives
The basic logic gates using one output and many inputs are used in Verilog. GATE uses one of the keywords - and, nand, or, nor, xor, xnor for use in Verilog for N number of inputs and 1 output.
Example: Module gate() Wire ot0; Wire ot1; Wire ot2; Reg in0,in1,in2,in3; Not U1(ot0,in0); Xor U2(ot1,in1,in2,in3); And U3(ot2, in2,in3,in0)
Transmission Gate Primitives
Transmission gate primitives include both, buffers and inverters. They have single input and one or more outputs. In the gate instantiation syntax shown below, GATE stands for either the keyword buf or NOT gate.
Example: Not, buf, bufif0, bufif1, notif0, notif1
Not – n outout inverter
Buf – n output buffer
Bufifo – tristate buffer, active low enable
Bufif1 – tristate buffer, active high enable
Notifo – tristate inverter, active low enable
Notif1 – tristate inverter, active high enable
Example: Module gate() Wire out0; Wire out1; Reg in0,in1; Not U1(out0,in0); Buf U2(out0,in0);
Data Types
Value Set
Verilog consists of, mainly, four basic values. All Verilog data types, which are used in Verilog store these values −
0 (logic zero, or false condition)
1 (logic one, or true condition)
x (unknown logic value)
z (high impedance state)
use of x and z is very limited for synthesis.
Wire
A wire is used to represent a physical wire in a circuit and it is used for connection of gates or modules. The value of a wire can only be read and not assigned in a function or block. A wire cannot store value but is always driven by a continuous assignment statement or by connecting wire to output of a gate/module. Other specific types of wires are −
Wand (wired-AND) − here value of Wand is dependent on logical AND of all the device drivers connected to it.
Wor (wired-OR) − here value of a Wor is dependent on logical OR of all the device drivers connected to it.
Tri (three-state) − here all drivers connected to a tri must be z, except only one (which determines value of tri).
Example: Wire [msb:lsb] wire_variable_list; Wirec // simple wire Wand d; Assign d = a; // value of d is the logical AND of Assign d = b; // a and b Wire [9:0] A; // a cable (vector) of 10 wires. Wand [msb:lsb] wand_variable_list; Wor [msb:lsb] wor_variable_list; Tri [msb:lsb] tri_variable_list;
Register
A reg (register) is a data object, which is holding the value from one procedural assignment to next one and are used only in different functions and procedural blocks. A reg is a simple Verilog, variable-type register and can't imply a physical register. In multi-bit registers, the data is stored in the form of unsigned numbers and sign extension is not used.
Example −
reg c; // single 1-bit register variable
reg [5:0] gem; // a 6-bit vector;
reg [6:0] d, e; // two 7-bit variables
Input, Output, Inout
These keywords are used to declare input, output and bidirectional ports of a task or module. Here input and inout ports, which are of wire type and output port is configured to be of wire, reg, wand, wor or tri type. Always, default is wire type.
Example
Module sample(a, c, b, d); Input c; // An input where wire is used. Output a, b; // Two outputs where wire is used. Output [2:0] d; /* A three-bit output. One must declare type in a separate statement. */ reg [1:0] a; // The above 'a' port is for declaration in reg.
Integer
Integers are used in general-purpose variables. They are used mainly in loops-indicies, constants, and parameters. They are of 'reg' type data type. They store data as signed numbers whereas explicitly declared reg types store them as an unsigned data. If the integer is not defined at the time of compiling, then the default size would be 32 bits.
If an integer holds a constant, the synthesizer adjusts them to the minimum width needed at the time of compilation.
Example
Integer c; // single 32-bit integer Assign a = 63; // 63 defaults to a 7-bit variable.
Supply0, Supply1
Supply0 define wires tied to logic 0 (ground) and supply1 define wires tied to logic 1 (power).
Example
supply0 logic_0_wires; supply0 gnd1; // equivalent to a wire assigned as 0 supply1 logic_1_wires; supply1 c, s;
Time
Time is a 64-bit quantity that can be used in conjunction with the $time system task to hold simulation time. Time is not supported for synthesis and hence is used only for simulation purposes.
Example
time time_variable_list; time c; c = $time; //c = current simulation time
Parameter
A parameter is defining a constant which can be set when you use a module, which allows customization of module during the instantiation process.
Example Parameter add = 3'b010, sub = 2'b11; Parameter n = 3; Parameter [2:0] param2 = 3'b110; reg [n-1:0] jam; /* A 3-bit register with length of n or above. */ always @(z) y = {{(add - sub){z}}; if (z) begin state = param2[1]; else state = param2[2]; end Operators
Arithmetic Operators
These operators is perform arithmetic operations. The + and −are used as either unary (x) or binary (z−y) operators.
The Operators which are included in arithmetic operation are −
+ (addition), −(subtraction), * (multiplication), / (division), % (modulus)
Example −
parameter v = 5; reg[3:0] b, d, h, i, count; h = b + d; i = d - v; cnt = (cnt +1)%16; //Can count 0 thru 15.
Relational Operators
These operators compare two operands and return the result in a single bit, 1 or 0.
Wire and reg variables are positive. Thus (−3'd001) = = 3'd111 and (−3b001)>3b110.
The Operators which are included in relational operation are −
- == (equal to)
- != (not equal to)
- > (greater than)
- >= (greater than or equal to)
- < (less than)
- <= (less than or equal to)
Example
if (z = = y) c = 1; else c = 0; // Compare in 2's compliment; d>b reg [3:0] d,b; if (d[3]= = b[3]) d[2:0] > b[2:0]; else b[3]; Equivalent Statement e = (z == y);
Bit-wise Operators
Bit-wise operators which are doing a bit-by-bit comparison between two operands.
The Operators which are included in Bit wise operation are −
- & (bitwise AND)
- | (bitwiseOR)
- ~ (bitwise NOT)
- ^ (bitwise XOR)
- ~^ or ^~(bitwise XNOR)
Example
module and2 (d, b, c); input [1:0] d, b; output [1:0] c; assign c = d & b; end module
Logical Operators
Logical operators are bit-wise operators and are used only for single-bit operands. They return a single bit value, 0 or 1. They can work on integers or group of bits, expressions and treat all non-zero values as 1. Logical operators are generally, used in conditional statements since they work with expressions.
The operators which are included in Logical operation are −
- ! (logical NOT)
- && (logical AND)
- || (logical OR)
Example
wire[7:0] a, b, c; // a, b and c are multibit variables. reg x; if ((a == b) && (c)) x = 1; //x = 1 if a equals b, and c is nonzero. else x = !a; // x =0 if a is anything but zero.
Reduction Operators
Reduction operators are the unary form of the bitwise operators and operate on all the bits of an operand vector. These also return a single-bit value.
The operators which are included in Reduction operation are −
- & (reduction AND)
- | (reduction OR)
- ~& (reduction NAND)
- ~| (reduction NOR)
- ^ (reduction XOR)
- ~^ or ^~(reduction XNOR)
Example
Module chk_zero (x, z); Input [2:0] x; Output z; Assign z = & x; // Reduction AND End module
Shift Operators
Shift operators, which are shifting the first operand by the number of bits specified by second operand in the syntax. Vacant positions are filled with zeros for both directions, left and right shifts (There is no use sign extension).
The Operators which are included in Shift operation are −
- << (shift left)
- >> (shift right)
Example
Assign z = c << 3; /* z = c shifted left 3 bits;
Vacant positions are filled with 0's */
Concatenation Operator
The concatenation operator combines two or more operands to form a larger vector.
The operator included in Concatenation operation is − { }(concatenation)
Example
wire [1:0] a, h; wire [2:0] x; wire [3;0] y, Z; assign x = {1'b0, a}; // x[2] = 0, x[1] = a[1], x[0] = a[0] assign b = {a, h}; /* b[3] = a[1], b[2] = a[0], b[1] = h[1], b[0] = h[0] */ assign {cout, b} = x + Z; // Concatenation of a result Replication Operator
The replication operator are making multiple copies of an item.
The operator used in Replication operation is − {n{item}} (n fold replication of an item)
Example
Wire [1:0] a, f; wire [4:0] x; Assign x = {2{1'f0}, a}; // Equivalent to x = {0,0,a } Assign y = {2{a}, 3{f}}; //Equivalent to y = {a,a,f,f} For synthesis, Synopsis did not like a zero replication. For example:- Parameter l = 5, k = 5; Assign x = {(l-k){a}} Conditional Operator
Conditional operator synthesizes to a multiplexer. It is the same kind as is used in C/C++ and evaluates one of the two expressions based on the condition.
The operator used in Conditional operation is −
(Condition) ? (Result if condition true) −
(result if condition false)
Example
Assign x = (g) ? a : b; Assign x = (inc = = 2) ? x+1 : x-1; /* if (inc), x = x+1, else x = x-1 */
Operands
Literals
Literals are constant-valued operands that are used in Verilog expressions. The two commonly used Verilog literals are −
-
String − A string literal operand is a one-dimensional array of characters, which are enclosed in double quotes (" ").
-
Numeric − A constant number operand is specified in binary, octal, decimal or hexadecimal Number.
Example
n − integer representing number of bits
F − one of four possible base formats −
b for binary, o for octal, d for decimal, h for hexadecimal.
"time is" // string literal 267 // 32-bit decimal number 2'b01 // 2-bit binary 20'hB36F // 20-bit hexadecimal number '062 // 32-bit octal number
Wires, Regs, and Parameters
Wires, regs and parameters are the data types used as operands in Verilog expressions.
Bit-Selection "x[2]" and Part-Selection "x[4:2]"
Bit-selects and part-selects are used to select one bit and a multiple bits, respectively, from a wire, reg or parameter vector with the use of square brackets "[ ]". Bit-selects and part-selects are also used as operands in expressions in the same way that their main data objects are used.
Example
reg [7:0] x, y; reg [3:0] z; reg a; a = x[7] & y[7]; // bit-selects z = x[7:4] + y[3:0]; // part-selects
Function Calls
In the Function calls, the return value of a function is used directly in an expression without the need of first assigning it to a register or wire. It just place the function call as one of the type of operands.it is needful to make sure you are knowing the bit width of the return value of function call.
Example Assign x = y & z & chk_yz(z, y); // chk_yz is a function . . ./* Definition of the function */ Function chk_yz; // function definition Input z,y; chk_yz = y^z; End function
Modules
Module Declaration
In Verilog, A module is the principal design entity. This indicates the name and port list (arguments). The next few lines which specifies the input/output type (input, output or inout) and width of the each port. The default port width is only 1 bit. The port variables must be declared by wire, wand,. . ., reg. The default port variable is wire. Normally, inputs are wire because their data is latched outside the module. Outputs are of reg type if their signals are stored inside.
Example
module sub_add(add, in1, in2, out); input add; // defaults to wire input [7:0] in1, in2; wire in1, in2; output [7:0] out; reg out; ... statements ... End module
Continuous Assignment
The continuous assignment in a Module is used for assigning a value on to a wire, which is the normal assignment used at outside of always or initial blocks. This assignment is done with an explicit assign statement or to assign a value to a wire during its declaration. Continuous assignment are continuously executed at the time of simulation. The order of assign statements does not affect it. If you do any change in any of the right-hand-side inputs signal it will change a left-hand-side output signal.
Example
Wire [1:0] x = 2'y01; // assigned on declaration Assign y = c | d; // using assign statement Assign d = a & b; /* the order of the assign statements does not matter. */
Module Instantiations
Module declarations are templates for creating actual objects. Modules are instantiated inside other modules, and each instantiation is creating a single object from that template. The exception is the top-level module which is its own instantiation. The module's ports must to be matched to those which are defined in the template. It is specified −
-
By name, using a dot ".template port name (name of wire connected to port)". Or
-
By position, placing the ports in the same place in the port lists of both of the template and the instance.
Example
MODULE DEFINITION Module and4 (x, y, z); Input [3:0] x, y; Output [3:0] z; Assign z = x | y; End module
Behavioural Modelling & Timing in Verilog
Behavioral models in Verilog contain procedural statements, which control the simulation and manipulate variables of the data types. These all statements are contained within the procedures. Each of the procedure has an activity flow associated with it.
During simulation of behavioral model, all the flows defined by the 'always' and 'initial' statements start together at simulation time 'zero'. The initial statements are executed once, and the always statements are executed repetitively. In this model, the register variables a and b are initialized to binary 1 and 0 respectively at simulation time 'zero'. The initial statement is then completed and is not executed again during that simulation run. This initial statement is containing a begin-end block (also called a sequential block) of statements. In this begin-end type block, a is initialized first followed by b.
Example of Behavioral Modeling
module behave; reg [1:0]a,b; initial begin a = 'b1; b = 'b0; end always begin #50 a = ~a; end always begin #100 b = ~b; end End module
Procedural Assignments
Procedural assignments are for updating reg, integer, time, and memory variables. There is a significant difference between procedural assignment and continuous assignment as described below −
Continuous assignments drive net variables and are evaluated and updated whenever an input operand changes value.
Procedural assignments update the value of register variables under the control of the procedural flow constructs that surround them.
The right-hand side of a procedural assignment can be any expression that evaluates to a value. However, part-selects on the right-hand side must have constant indices. The lefthand side indicates the variable that receives the assignment from the right-hand side. The left-hand side of a procedural assignment can take one of the following forms −
-
register, integer, real, or time variable − An assignment to the name reference of one of these data types.
-
bit-select of a register, integer, real, or time variable − An assignment to a single bit that leaves the other bits untouched.
-
part-select of a register, integer, real, or time variable − A part-select of two or more contiguous bits that leaves the rest of the bits untouched. For the part-select form, only constant expressions are legal.
-
memory element − A single word of a memory. Note that bit-selects and part-selects are illegal on memory element references.
-
concatenation of any of the above − A concatenation of any of the previous four forms can be specified, which effectively partitions the result of the right-hand side expression and assigns the partition parts, in order, to the various parts of the concatenation.
Delay in Assignment (not for synthesis)
In a delayed assignment Δt time units pass before the statement is executed and the lefthand assignment is made. With intra-assignment delay, the right side is evaluated immediately but there is a delay of Δt before the result is place in the left hand assignment. If another procedure changes a right-hand side signal during Δt, it does not effect the output. Delays are not supported by synthesis tools.
Syntax
-
Procedural Assignment variable = expression
-
Delayed assignment #Δt variable = expression;
-
Intra-assignment delay variable = #Δt expression;
Example
reg [6:0] sum; reg h, ziltch; sum[7] = b[7] ^ c[7]; // execute now. ziltch = #15 ckz&h; /* ckz&a evaluated now; ziltch changed after 15 time units. */ #10 hat = b&c; /* 10 units after ziltch changes, b&c is evaluated and hat changes. */
Blocking Assignments
A blocking procedural assignment statement must be executed before the execution of the statements that follow it in a sequential block. A blocking procedural assignment statement does not prevent the execution of statements that follow it in a parallel block.
Syntax
The syntax for a blocking procedural assignment is as follows −
<lvalue> = <timing_control> <expression>
Where, lvalue is a data type that is valid for a procedural assignment statement, = is the assignment operator, and timing control is the optional intra - assignment delay. The timing control delay can be either a delay control (for example, #6) or an event control (for example, @(posedge clk)). The expression is the right-hand side value the simulator assigns to the left-hand side. The = assignment operator used by blocking procedural assignments is also used by procedural continuous assignments and continuous assignments.
Example
rega = 0; rega[3] = 1; // a bit-select rega[3:5] = 7; // a part-select mema[address] = 8'hff; // assignment to a memory element {carry, acc} = rega + regb; // a concatenation Nonblocking (RTL) Assignments
The non-blocking procedural assignment allows you to schedule assignments without blocking the procedural flow. You can use the non-blocking procedural statement whenever you want to make several register assignments within the same time step without regard to order or dependance upon each other.
Syntax
The syntax for a non-blocking procedural assignment is as follows −
<lvalue> <= <timing_control> <expression>
Where lvalue is a data type that is valid for a procedural assignment statement, <= is the non-blocking assignment operator, and timing control is the optional intra-assignment timing control. The timing control delay can be either a delay control or an event control (for example, @(posedge clk)). The expression is the right-hand side value the simulator assigns to the left-hand side. The non-blocking assignment operator is the same operator the simulator uses for the less-than-orequal relational operator. The simulator interprets the <= operator to be a relational operator when you use it in an expression, and interprets the <= operator to be an assignment operator when you use it in a non-blocking procedural assignment construct.
How the simulator evaluates non-blocking procedural assignments When the simulator encounters a non-blocking procedural assignment, the simulator evaluates and executes the non-blocking procedural assignment in two steps as follows −
-
The simulator evaluates the right-hand side and schedules the assignment of the new value to take place at a time specified by a procedural timing control. The simulator evaluates the right-hand side and schedules the assignment of the new value to take place at a time specified by a procedural timing control.
-
At the end of the time step, in which the given delay has expired or the appropriate event has taken place, the simulator executes the assignment by assigning the value to the left-hand side.
Example
module evaluates2(out); output out; reg a, b, c; initial begin a = 0; b = 1; c = 0; end always c = #5 ~c; always @(posedge c) begin a <= b; b <= a; end endmodule
Conditions
The conditional statement (or if-else statement) is used to make a decision as to whether a statement is executed or not.
Formally, the syntax is as follows −
<statement> ::= if ( <expression> ) <statement_or_null> ||= if ( <expression> ) <statement_or_null> else <statement_or_null> <statement_or_null> ::= <statement> ||= ;
The <expression> is evaluated; if it is true (that is, has a non-zero known value), the first statement executes. If it is false (has a zero value or the value is x or z), the first statement does not execute. If there is an else statement and <expression> is false, the else statement executes. Since, the numeric value of the if expression is tested for being zero, certain shortcuts are possible.
For example, the following two statements express the same logic −
if (expression) if (expression != 0)
Since, the else part of an if-else is optional, there can be confusion when an else is omitted from a nested if sequence. This is resolved by always associating the else with the closest previous if that lacks an else.
Example
if (index > 0) if (rega > regb) result = rega; else // else applies to preceding if result = regb; If that association is not what you want, use a begin-end block statement to force the proper association if (index > 0) begin if (rega > regb) result = rega; end else result = regb;
Construction of: if- else- if
The following construction occurs so often that it is worth a brief separate discussion.
Example
if (<expression>) <statement> else if (<expression>) <statement> else if (<expression>) <statement> else <statement>
This sequence of if's (known as an if-else-if construct) is the most general way of writing a multi-way decision. The expressions are evaluated in order; if any expression is true, the statement associated with it is executed, and this terminates the whole chain. Each statement is either a single statement or a block of statements.
The last else part of the if-else-if construct handles the 'none of the above' or default case where none of the other conditions was satisfied. Sometimes there is no explicit action for the default; in that case, the trailing else can be omitted or it can be used for error checking to catch an impossible condition.
Case Statement
The case statement is a special multi-way decision statement that tests whether an expression matches one of a number of other expressions, and branches accordingly. The case statement is useful for describing, for example, the decoding of a microprocessor instruction. The case statement has the following syntax −
Example
<statement> ::= case ( <expression> ) <case_item>+ endcase ||= casez ( <expression> ) <case_item>+ endcase ||= casex ( <expression> ) <case_item>+ endcase <case_item> ::= <expression> <,<expression>>* : <statement_or_null> ||= default : <statement_or_null> ||= default <statement_or_null>
The case expressions are evaluated and compared in the exact order in which they are given. During the linear search, if one of the case item expressions matches the expression in parentheses, then the statement associated with that case item is executed. If all comparisons fail, and the default item is given, then the default item statement is executed. If the default statement is not given, and all of the comparisons fail, then none of the case item statements is executed.
Apart from syntax, the case statement differs from the multi-way if-else-if construct in two important ways −
-
The conditional expressions in the if-else-if construct are more general than comparing one expression with several others, as in the case statement.
-
The case statement provides a definitive result when there are x and z values in an expression.
Looping Statements
There are four types of looping statements. They provide a means of controlling the execution of a statement zero, one, or more times.
-
forever continuously executes a statement.
-
repeat executes a statement a fixed number of times.
-
while executes a statement until an expression becomes false. If the expression starts out false, the statement is not executed at all.
-
for controls execution of its associated statement(s) by a three-step process, as follows −
-
Executes an assignment normally used to initialize a variable that controls the number of loops executed
-
Evaluates an expression—if the result is zero, the for loop exits, and if it is not zero, the for loop executes its associated statement(s) and then performs step 3
-
Executes an assignment normally used to modify the value of the loopcontrol variable, then repeats step 2
-
The following are the syntax rules for the looping statements −
Example
<statement> ::= forever <statement> ||=forever begin <statement>+ end <Statement> ::= repeat ( <expression> ) <statement> ||=repeat ( <expression> ) begin <statement>+ end <statement> ::= while ( <expression> ) <statement> ||=while ( <expression> ) begin <statement>+ end <statement> ::= for ( <assignment> ; <expression> ; <assignment> ) <statement> ||=for ( <assignment> ; <expression> ; <assignment> ) begin <statement>+ end
Delay Controls
Delay Control
The execution of a procedural statement can be delay-controlled by using the following syntax −
<statement> ::= <delay_control> <statement_or_null> <delay_control> ::= # <NUMBER> ||= # <identifier> ||= # ( <mintypmax_expression> )
The following example delays the execution of the assignment by 10 time units −
#10 rega = regb;
The next three examples provide an expression following the number sign (#). Execution of the assignment delays by the amount of simulation time specified by the value of the expression.
Event Control
The execution of a procedural statement can be synchronized with a value change on a net or register, or the occurrence of a declared event, by using the following event control syntax −
Example
<statement> ::= <event_control> <statement_or_null> <event_control> ::= @ <identifier> ||= @ ( <event_expression> ) <event_expression> ::= <expression> ||= posedge <SCALAR_EVENT_EXPRESSION> ||= negedge <SCALAR_EVENT_EXPRESSION> ||= <event_expression> <or <event_expression>>
*<SCALAR_EVENT_EXPRESSION> is an expression that resolves to a one bit value.
Value changes on nets and registers can be used as events to trigger the execution of a statement. This is known as detecting an implicit event. Verilog syntax also allows you to detect change based on the direction of the change—that is, toward the value 1 (posedge) or toward the value 0 (negedge). The behaviour of posedge and negedge for unknown expression values is as follows −
- a negedge is detected on the transition from 1 to unknown and from unknown to 0
- a posedge is detected on the transition from 0 to unknown and from unknown to 1
Procedures: Always and Initial Blocks
All procedures in Verilog are specified within one of the following four Blocks. 1) Initial blocks 2) Always blocks 3) Task 4) Function
The initial and always statements are enabled at the beginning of simulation. The initial blocks executes only once and its activity dies when the statement has finished. In contrast, the always blocks executes repeatedly. Its activity dies only when the simulation is terminated. There is no limit to the number of initial and always blocks that can be defined in a module. Tasks and functions are procedures that are enabled from one or more places in other procedures.
Initial Blocks
The syntax for the initial statement is as follows −
<initial_statement> ::= initial <statement>
The following example illustrates the use of the initial statement for initialization of variables at the start of simulation.
Initial Begin Areg = 0; // initialize a register For (index = 0; index < size; index = index + 1) Memory [index] = 0; //initialize a memory Word End
Another typical usage of the initial Blocks is specification of waveform descriptions that execute once to provide stimulus to the main part of the circuit being simulated.
Initial Begin Inputs = 'b000000; // initialize at time zero #10 inputs = 'b011001; // first pattern #10 inputs = 'b011011; // second pattern #10 inputs = 'b011000; // third pattern #10 inputs = 'b001000; // last pattern End
Always Blocks
The 'always' statement repeats continuously throughout the whole simulation run. The syntax for the always statement is given below
<always_statement> ::= always <statement>
The 'always' statement, because of its looping nature, is only useful when used in conjunction with some form of timing control. If an 'always' statement provides no means for time to advance, the 'always' statement creates a simulation deadlock condition. The following code, for example, creates an infinite zero-delay loop −
Always areg = ~areg;
Providing a timing control to the above code creates a potentially useful description—as in the following example −
Always #half_period areg = ~areg;
Tanner Tool For Vlsi Design
Source: https://www.tutorialspoint.com/vlsi_design/vlsi_design_quick_guide.htm
Posted by: hydesith1974.blogspot.com

0 Response to "Tanner Tool For Vlsi Design"
Post a Comment